Capitolo 8 Introduzione ai Modelli Mistura Gaussiani (MM)
8.1 Introduzione
I metodi di clustering descritti finora non si basano su modelli formali per la struttura dei cluster nei dati. Questo può rendere difficoltosa o arbitraria la scelta del metodo, la stima del numero di cluster, ecc. Se poi volessimo usare la soluzione di clustering a fini predittivi, senza un modello l’inferenza formale ci risulterebbe sostanzialmente preclusa.
Uno degli approcci di clustering che postula un modello statistico formale per la popolazione da cui sono campionati i dati, è noto come modello di misture finite di densità. Questo modello postula che la popolazione complessiva sia in realtà formata da un numero di sottopopolazioni (i “cluster”), ciascuna con una funzione di densità di probabilità multivariata differente. Adottando questo approccio, il problema di clustering diventa quello di stimare i parametri della mistura assunta, e quindi usare i parametri stimati per calcolare le probabilità (a posteriori) di appartenenza ai cluster per ciascun item. Inoltre, la determinazione del numero di cluster si riduce ad un problema di selezione del modello per cui esistono procedure oggettive. L’analisi dei cluster basata su modelli mustura finiti sono anche noti come metodi di clustering model-based (basati su modello).
Usualmente i parametri delle delnsità delle sottopopolazioni sono stimati con la massima verosimiglianza usando l’algoritmo di expectation-maximization (EM).
Fraley e Raftery (Model-based clustering, discriminant analysis, and
density estimation, Journal of the American Statistical Association, 97,
611-631) hanno sviluppato una serie di modelli mistura finiti di densità normali multivariate
in cui si lasciano variare tra cluster alcune delle caratteristiche delle matrici di
covarianza, mantenendone nel contempo altre fisse. Questo approccio è
implementato per esempio nel package mclust, ma molti altri package sono stati sviluppati
in questo campo (si veda la task view del CRAN sulla cluster analysis all’indirizzo
http://cran.r-project.org/web/views/Cluster.html).
8.2 Esempio: dati faithful
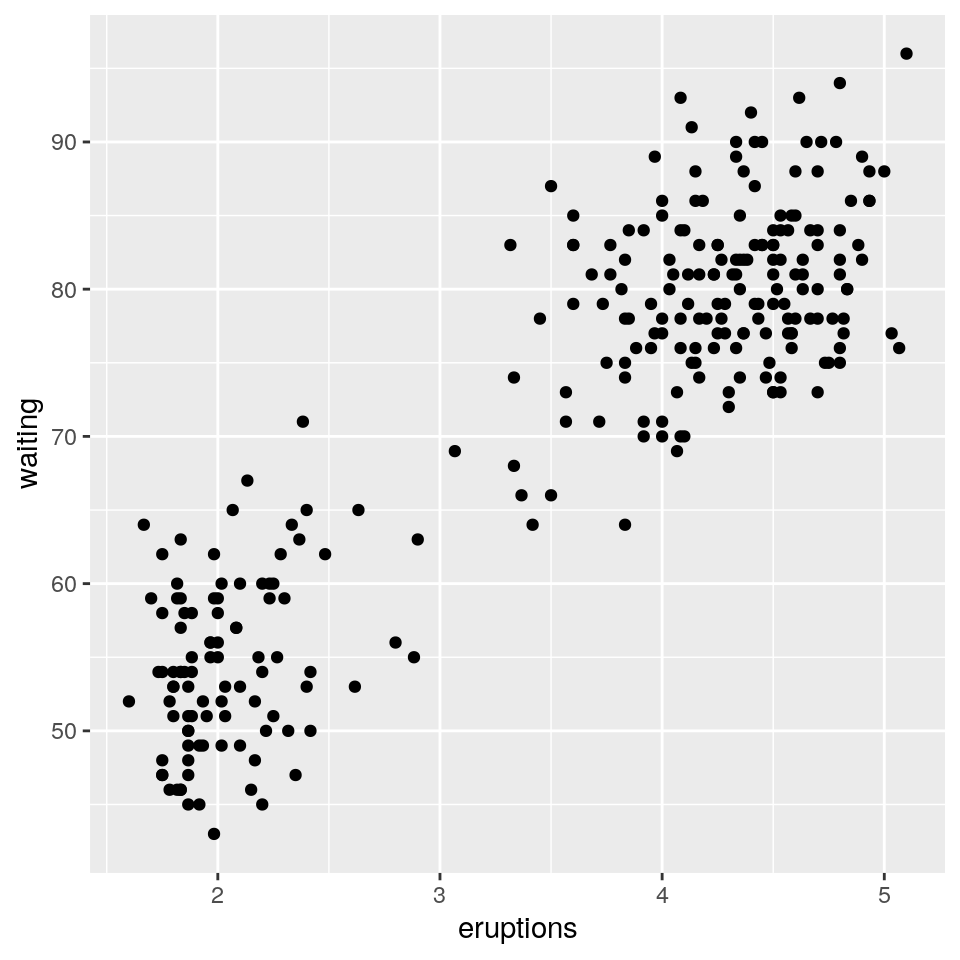
La funzione per eseguire un’analisi dei cluster è Mclust(). Come esempio, consideriamo il dataset
bivariato faithful incluso nella distribuzione base di R.
Questo dataset contiene il tempo d’attesa e la durata delle eruzioni per il geyser Old Faithful nello Yellowstone National Park, Wyoming, USA.
## ----------------------------------------------------
## Gaussian finite mixture model fitted by EM algorithm
## ----------------------------------------------------
##
## Mclust EEE (ellipsoidal, equal volume, shape and orientation) model with 3
## components:
##
## log-likelihood n df BIC ICL
## -1126.326 272 11 -2314.316 -2357.824
##
## Clustering table:
## 1 2 3
## 40 97 135In questo caso, il miglior modello, in accordo con il criterio BIC (Bayesian Information Criterion) è il modello con 3 componenti (cioè, cluster) e matrici di varianza/covarianza uguali nei cluster (elissoidali, con volume, forma e orientamento uguali). Possiamo ottenere un riepilogo più dettagliato, inclusi i parametri stimati, usando il seguente codice
## ----------------------------------------------------
## Gaussian finite mixture model fitted by EM algorithm
## ----------------------------------------------------
##
## Mclust EEE (ellipsoidal, equal volume, shape and orientation) model with 3
## components:
##
## log-likelihood n df BIC ICL
## -1126.326 272 11 -2314.316 -2357.824
##
## Clustering table:
## 1 2 3
## 40 97 135
##
## Mixing probabilities:
## 1 2 3
## 0.1656784 0.3563696 0.4779520
##
## Means:
## [,1] [,2] [,3]
## eruptions 3.793066 2.037596 4.463245
## waiting 77.521051 54.491158 80.833439
##
## Variances:
## [,,1]
## eruptions waiting
## eruptions 0.07825448 0.4801979
## waiting 0.48019785 33.7671464
## [,,2]
## eruptions waiting
## eruptions 0.07825448 0.4801979
## waiting 0.48019785 33.7671464
## [,,3]
## eruptions waiting
## eruptions 0.07825448 0.4801979
## waiting 0.48019785 33.7671464I risultati del clustering possono essere visualizzati graficamente con
op <- par(mfrow = c(2, 2))
plot(faithfulMclust, what = "BIC")
plot(faithfulMclust, what = "classification")
plot(faithfulMclust, what = "uncertainty")
plot(faithfulMclust, what = "density")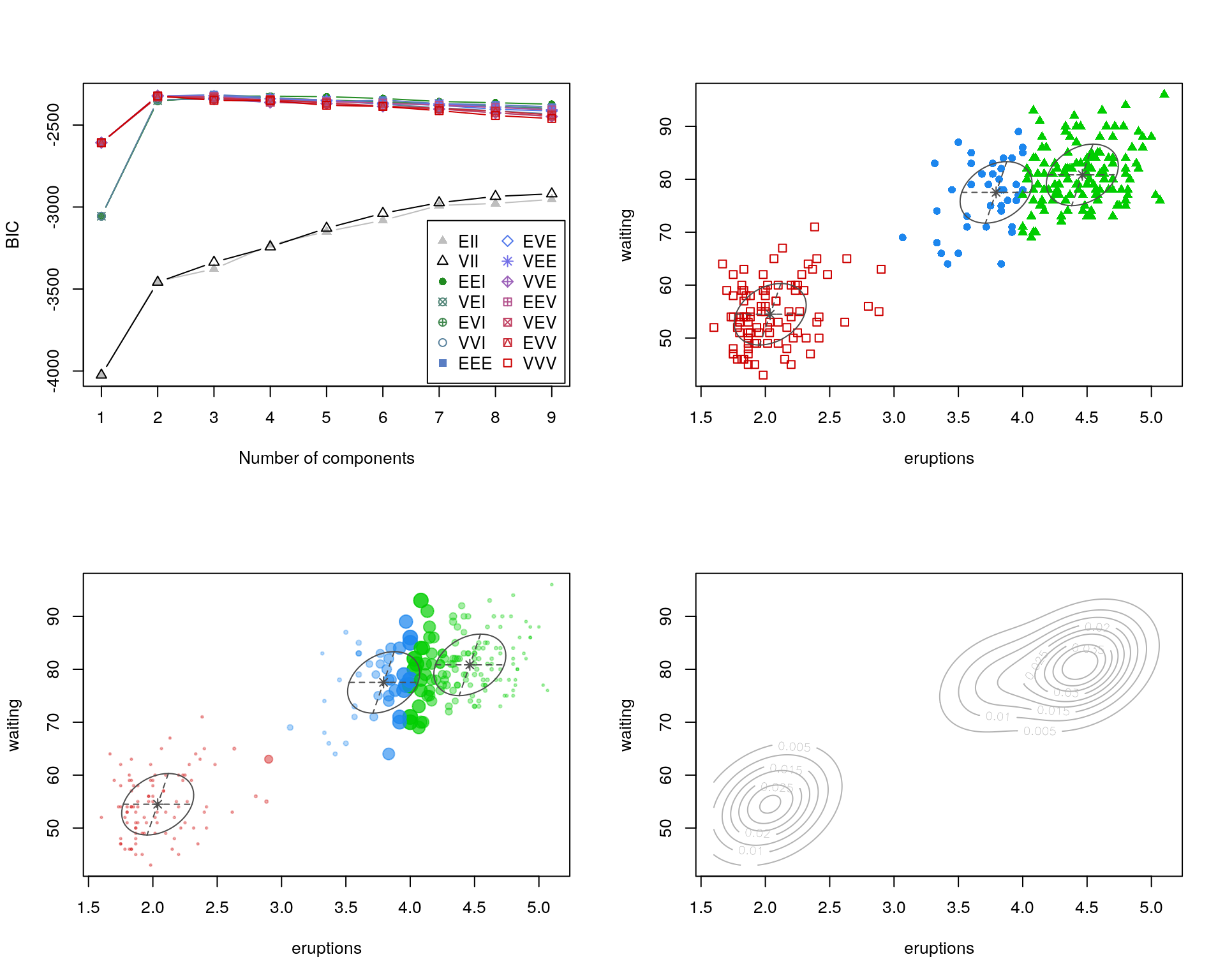
Per impostazione predefinita la funzione Mclust() confronta i valori di BIC per parametri
ottimizzati fino ad un massimo di nove componenti, con tutte le strutture di covarianza
attualmente disponibili nel software (sottografico in alto a sinistra). L’output include i parametri del modello che
ottiene il BIC massimo (dove il massimo è calcolato su tutti i modelli e
il numero di componenti considerate), e la corrispondente classificazione (sottografico in alto a destra) e
incertezza (sottografico in basso a sinistra, dove la dimensione dei punti rappresenta l’incertezza nella classificazione).
Qualunque valore di dato mancante (cioè, NA) ritornato dall’output corrisponde
a modelli e a numeri di cluster per cui non è stato possibile calcolare valori di parametri.
Il sottografico in basso a destra mostra la densità di probabilità multivariata congiunta per tutti i gruppi.
La lista con la descrizione dei modelli disponibili nel package mclust è facilmente ottenibile con
Ed i modelli attualmente disponibli sono:
Mistura univariata
“E” = varianze uguali (unidimensionali)
“V” = varianze variabili (unidimensionali)
Mistura multivariata
“EII” = sferica, volume uguale
“VII” = sferica, volume variabile
“EEI” = diagonale, uguali volume e forma
“VEI” = diagonale, volume variabile, forma uguale
“EVI” = diagonale, volume uguale, forma variabile
“VVI” = diagonale, volume e forma variabili
“EEE” = ellissoidale, uguali volume, forma e orientamento
“EVE” = ellissoidale, uguali volume e orientamento
“VEE” = ellissoidale, uguali forma e orientamento
“VVE” = ellissoidale, uguale orientamento
“EEV” = ellissoidale, uguali volume e forma
“VEV” = ellissoidale, uguale forma
“EVV” = ellissoidale, uguale volume
“VVV” = ellissoidale, variabili volume, forma e orientamento
Componente singola
“X” = normale univariata
“XII” = normale multivariata sferica
“XXI” = normale multivariata diagonale
“XXX” = normale multivariata ellissoidale
Per avere più dettagli sulle tante funzionalità del package mclust, si vedano le
pagine di help del package:
8.3 Alcuni cenni di teoria
Il Modello Mistura Normale assume che i dati provengano da una mistura finita di \(G\) \(p\)-multivariate distribuzioni normali, cioè, che la densità della popolazione possa essere espressa come: \[ f(\underline{y};\underline\theta,\underline\tau)=\sum_{k=1}^G {\tau_k f_k(\underline{y};\theta_k)} \] dove \(f_k\) e \(\theta_k\) sono la densità ed i parametri della \(k\)-ma componente di mistura, e \(\tau_k\) è la probabilità che l’osservazione \(\underline{y}\) appartenga alla \(k\)-ma componente (\(\tau_k \ge 0; \sum_{k=1}^G {\tau_k}=1\)), e \(f_k\) è una funzione di densità Normale multivariata, dove \(\theta_k\) è il parametro dato da \(\underline\mu_k, \Sigma_k\): \[ f_k(\underline{y}| \underline\mu_k, \Sigma_k)=\dfrac{\exp\left \{ -\frac{1}{2}(\underline{y}-\underline{\mu_k})^T \Sigma_k^{-1} (\underline{y}-\underline{\mu_k}) \right \}}{(2 \pi)^{\frac{p}{2}} \sqrt{ |\Sigma_k|}} \]
\(\tau_k\) e \(\theta_k\) (cioè \(\underline{\mu}_k\) e \(\Sigma_k\)) sono parametri ignoti.
Il processo di stima assume che i dati completi siano, in effetti, dati da sue insiemi di osservazioni per ciascuna osservazione (\(i=1, \cdots,n\)): \(\underline{x_i}=(\underline{y}_i^T,\underline{z}_i^T)^T\).
Dove \(\underline{y}_i\) sono i dati osservati per l’\(i\)-ma unità campionaria, e \(\underline{z}_i\) è un vettore \(G\)-dimensionale non osservabile di valori \(0/1\), che assume valore 1 in corrispondenza al solo elemento di appartenenza alla specifica (\(k\)-ma) componente.
Date le definizioni qui sopra, possiamo scrivere la log-verosimiglianza dei dati come:
\[
\ell(\underline{\theta},\underline{\tau},\underline{z}_i|\underline{x})=\sum_{i=1}^n{\log \left[ \sum_{k=1}^G{z_{ik} \tau_k f_k(y_i|\theta_k)} \right]}
\]
Dove \(\underline{z}_i\) significa che abbiamo un vettore non osservabile \(\underline{z}\) per ciascuna osservazione. Questi valori Such values have devono essere stimati insieme a \(\underline{\theta}\) (dove \(\theta_k\) in questo caso rappresenta il “parametro congiunto” \((\underline\mu_k, \Sigma_k)\)) e \(\underline{\tau}_k\) (\(k=1, \cdots, G\)).
Per stimare i parametri ignoti e le variabili non osservabili è usato un algortimo EM .
Il criterio usato per selezionare il numero di componenti (cluster) della mistura Gaussiana è il Bayesian Information Criterion (BIC): \[BIC = 2 \ell(\underline{\hat\theta},\underline{\hat\tau},\underline{\hat{z}}_i|\underline{x}) - (\# parameters) \cdot \log(n)\] Dove \(\ell(\underline{\hat\theta},\underline{\hat\tau},\underline{\hat{z}}_i|\underline{x})\) è il valore massimizzato della log-verosimiglianza, \((\# parameters)\) è il numero di parametri stimati, e \(n\) è la dimensione campionaria. Si noti che l’indice BIC, generalmente, è definito con il segno opposto rispetto alla definizione usata in questo package (e quindi, indice più piccolo => migliore).