Capitolo 10 Introduzione all’algoritmo Affinity Propagation
10.1 Introduzione
In statistica e data mining, affinity propagation (AP) è un algoritmo di clustering basato sul concetto di “passaggio di messaggi” tra punti (item). Diversamente dagli algoritmi di clustering quali il k-means, affinity propagation non richiede che sia definito a priori, o stimato prima di esegire l’algoritmo, il numero di cluster. Affinity propagation, in maniera simile al k-medoids (non ancora trattato, ma magari in futuro…) cerca membri “rappresentativi” (“exemplars”) dell’insieme di input, che siano, appunto, rappresentativi dei singoli cluster.
10.2 Esempio: dati iris
Carichiamo il package apcluster, il package scelto per l’applicazione dell’algoritmo di affinity propagation:
Prendiamo i dati di iris e teniamo solo le colonne delle misurazioni numeriche, trasformandolo poi in matrice, come nell’esempio precedente:
Possiamo quindi lanciare la procedura di clustering in maniera molto semplice:
In questo esempio, la funzione apcluster() calcola prima una matrice di somiglianza per i dati di input
iris usando la funzione di somiglianza passata come primo argomento. La scelta negDistMat(r=2) corrisponde alla
misura di somiglianza standard usata negli articoli di Frey and Dueck: il negativo delle distanze euclidee al quadrato.
Ovviamente, in alternativa si può calcolare prima la matrice di somiglianza e quindi chiamare apcluster() per la
matrice di somiglianza calcolata:
Possiamo ora visualizzare il risultato del calcolo del clustering semplicemente chiedendo di visualizzare l’oggetto apres1a (o apres1b):
##
## APResult object
##
## Number of samples = 150
## Number of iterations = 162
## Input preference = -5.57
## Sum of similarities = -45.96
## Sum of preferences = -33.42
## Net similarity = -79.38
## Number of clusters = 6
##
## Exemplars:
## 8 55 70 106 113 139
## Clusters:
## Cluster 1, exemplar 8:
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
## 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
## Cluster 2, exemplar 55:
## 51 52 53 55 59 66 69 73 74 75 76 77 78 87 88 98 120 134
## Cluster 3, exemplar 70:
## 54 58 60 61 63 65 68 70 72 80 81 82 83 89 90 91 93 94 95 96 97 99 100 107
## Cluster 4, exemplar 106:
## 106 108 110 118 119 123 131 132 136
## Cluster 5, exemplar 113:
## 101 103 104 105 109 111 112 113 116 117 121 125 126 129 130 133 137 138 140
## 141 142 144 145 146 148 149
## Cluster 6, exemplar 139:
## 56 57 62 64 67 71 79 84 85 86 92 102 114 115 122 124 127 128 135 139 143
## 147 150L’output dell’analisi individua 6 gruppi, di cui i punti rappresentativi (exemplar) sono gli item alle righe 8, 55, 70, 106, 113, 139.
Possiamo anche rappresentare graficamente i risultati, indicando il modello di raggruppamento e i dati:
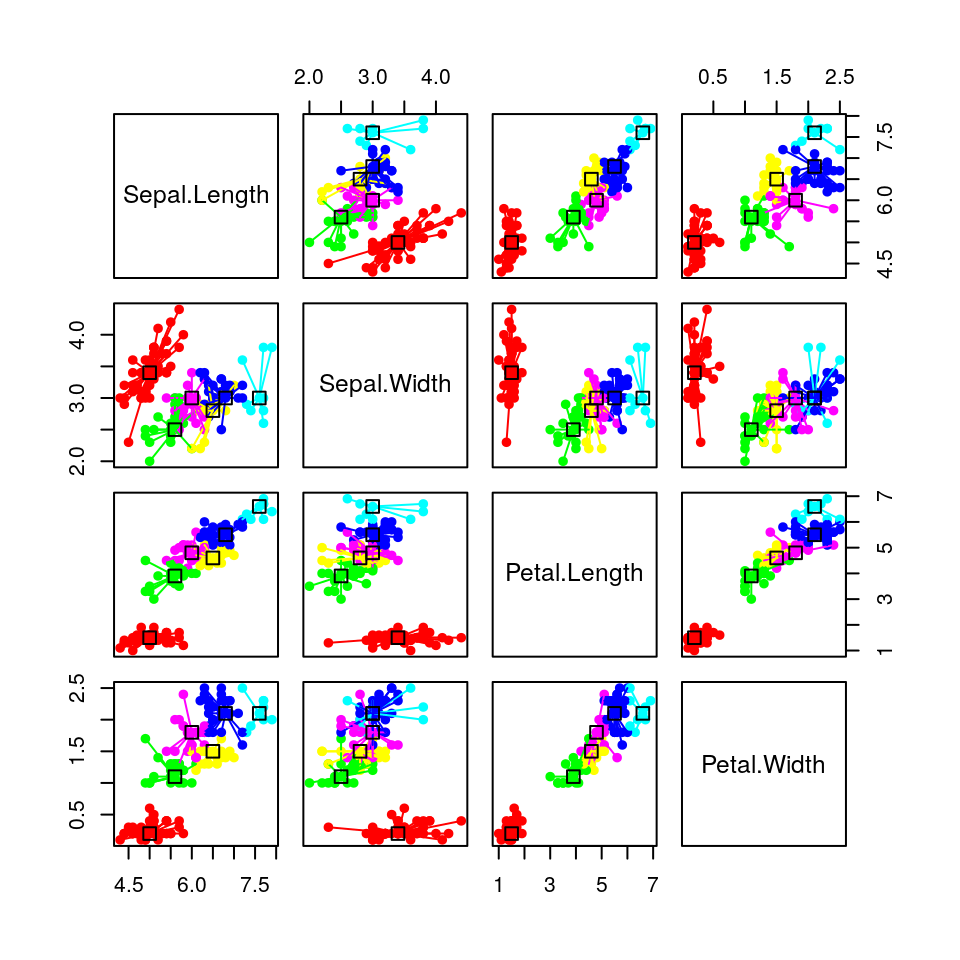
In questo grafico, ogni colore rappresenta un cluster. L’exemplar di ciascun cluster è rappresentato con un
“quadratino” e tutti i membri del cluster sono connessi ai loro exemplar con linee.
E’ anche possibile tracciare una heatmap dei punti, con heatmap():
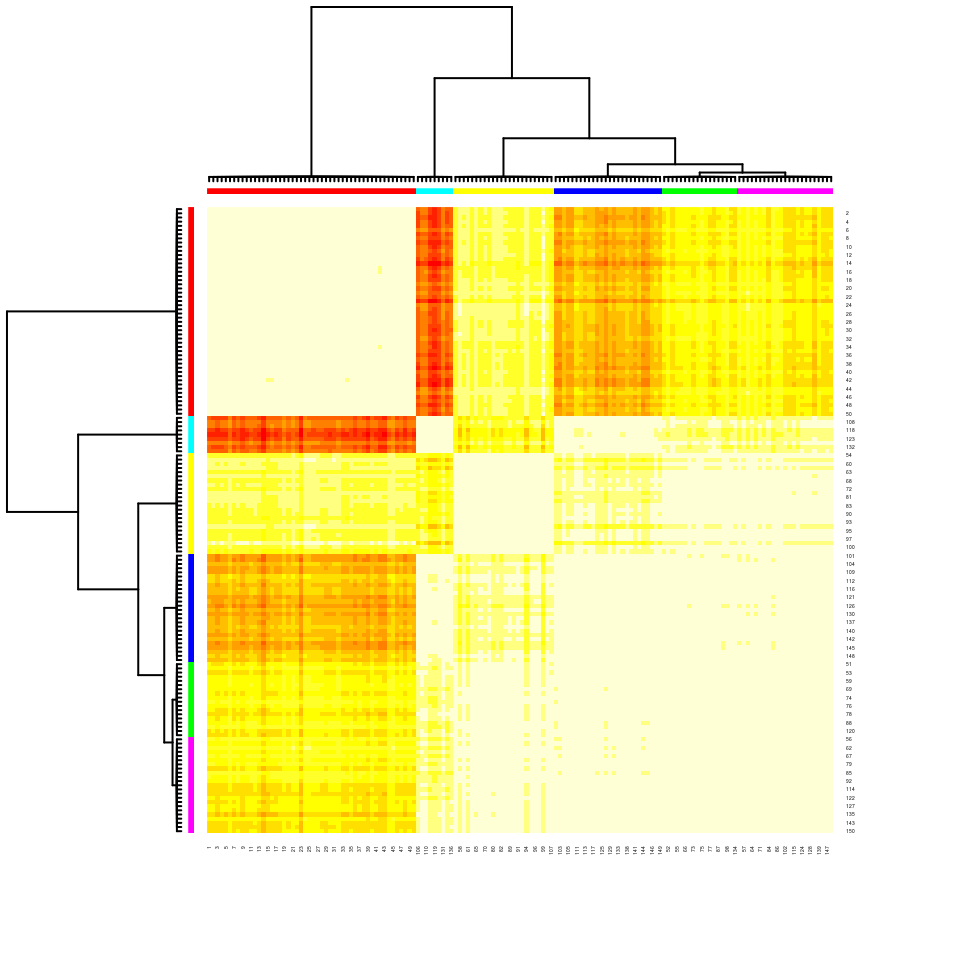
Nella hetmap i singoli item sono rappresentati sulle righe e colonne del grafico. I dendrogrammi (con i relativi colori) permettono di identificare i sottogruppi e le distanze reltive tra sottogruppi. I colori interni al grafico, invece, mostrano le distanze tra i singoli item: dal bianco (distanza minima) al rosso (distanza massima), passando per giallo, arancione, ecc..
Possiamo ora provare a vedere se è possibile ottenere un raggruppamento meno granulare dei nostri item.
Per fare questo possiamo impostare il valore minimo delle somiglianze fuori diagonale (q = 0, che indica
il quantile 0 dei valori di somiglianza non infiniti; si veda nel prossimo paragrafo una
spiegazione del metodo dell’affinity propagation):
##
## APResult object
##
## Number of samples = 150
## Number of iterations = 126
## Input preference = -50.2
## Sum of similarities = -84.44
## Sum of preferences = -150.6
## Net similarity = -235.04
## Number of clusters = 3
##
## Exemplars:
## 8 56 113
## Clusters:
## Cluster 1, exemplar 8:
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
## 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
## Cluster 2, exemplar 56:
## 52 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 79
## 80 81 82 83 84 85 86 88 89 90 91 92 93 94 95 96 97 98 99 100 102 107 114
## 120 122 124 127 128 134 139 143 150
## Cluster 3, exemplar 113:
## 51 53 77 78 87 101 103 104 105 106 108 109 110 111 112 113 115 116 117 118
## 119 121 123 125 126 129 130 131 132 133 135 136 137 138 140 141 142 144 145
## 146 147 148 149Il numero di cluster individuati diventa 3.
Possiamo quindi provare a rappresentare i gruppi così ottenuti:
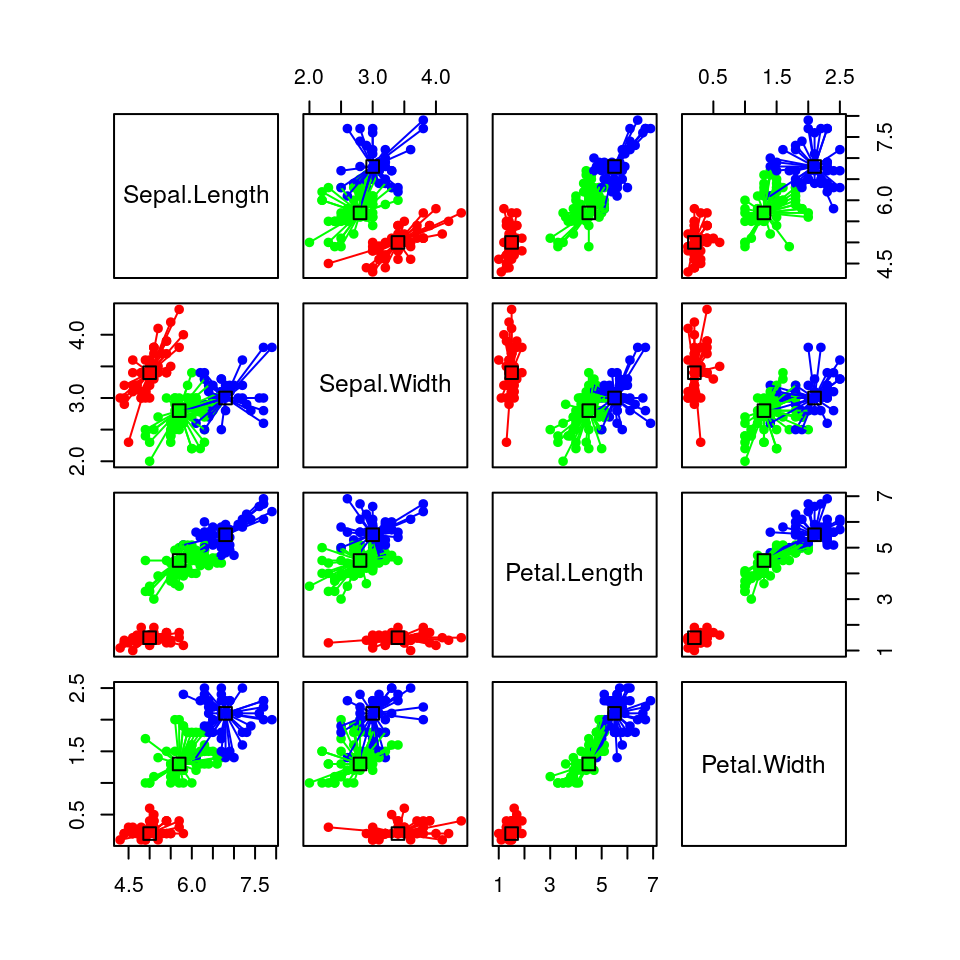
… e la relativa heatmap:
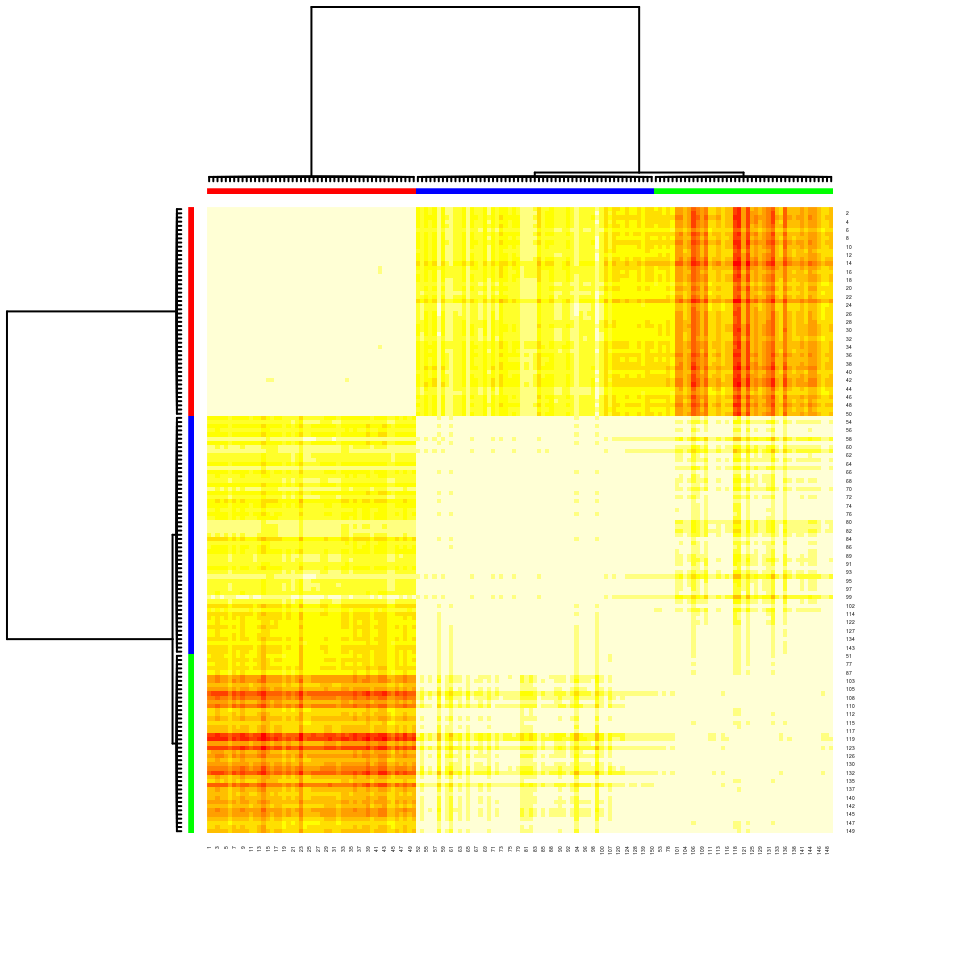
Infine, giusto per curiosità, possiamo provare ad verificare quanto il raggruppamento così individuato può corrispondere ai tipi di iris:
## species
## setosa versicolor virginica
## 8 50 0 0
## 56 0 45 12
## 113 0 5 38Come possiamo vedere la specie setosa è ben rappresentata dall’exemplar della riga 8 (e questo è confermato anche dai colori dell’heatmap), mentre gli exemplar delle righe 56 e 113, rispettivamente rappresentano con un certo grado di sovrapposizione le specie versicolor e virginica.
10.3 L’algoritmo in breve
L’algoritmo di affinity propagation si basa su uno schema di passaggio di messaggi in cui gli item competono per diventare exemplar. Il senso intuitivo dell’algoritmo non mi è ancora del tutto chiaro, ma mi riprometto di approfondirne il significato e quindi fornirne una spiegazione un po’ più intuitiva.
Sia \(x_i (i = 1, \dots, n)\) un insieme di punti vettoriali (item), senza assunti sulla loro struttura interna, e sia \(s\) una funzione che quantifica la somiglianza (similarity) tra due punti qualunque; \(s\) deve essere tale per cui \(s(x_i, x_j) > s(x_i, x_k)\) se e solo se \(x_i\) è più simile a \(x_j\) che a \(x_k\). Per questo esempio, useremo per \(s\) il negativo della distanza euclidea al quadrato tra due punti, cioè, per i punti \(x_i\) e \(x_k\), \(s(i,k)=-\left\|x_{i}-x_{k}\right\|^{2}\)
La diagonale di \(s\) (cioè \(s(i,i)\)) contiene le “self-similarities” (auto-somiglianze), chiamate anche input preference; la diagonale è particolarmente importante, poiché determina le tendenze individuali degli item a diventare “rappresentativi” (exemplar). Quando la diagonale è impostata sullo stesso valore per tutti gli input, controlla quante classi l’algoritmo potrà produrre. Un valore prossimo alla minima somiglianza possibile produce meno classi, mentre un valore prossimo o più grande della somiglianza più grande possibile, produce molte classi. Il valore è tipicamente inizializzato al valore di somiglianza mediana tra tutte le coppie di input.
L’algoritmo procede alternando due step di passaggio di messaggi, per aggiornare due matrici:
- La matrice di “responsabilità” (“responsibility”) \(\mathbb{R}\) ha valori \(r(i, k)\), che quantificano quanto \(x_k\) è adeguato come exemplar per \(x_i\), tenendo in considerazione tutti altri candidati exemplar per \(x_i\).
- La matrice di “disponibilità” (“availability”) \(\mathbb{A}\) contiene valori \(a(i, k)\), che rappresentano quanto sarebbe “appropriato” per \(x_i\) impostare \(x_k\) come suo exemplar, tenendo in considerazione la preferenza degli altri punti, come exemplar per \(x_k\).
Entrambe le matrici sono inzializzate con tutti valori zero, e possono essere viste come tabelle di log-probabilità. L’algoritmo quindi esegue iterativamente i seguenti aggiornamenti:
- Sono prima inviati gli aggiornamenti di responsabilità: \(r(i,k) \leftarrow s(i,k) - \max_{k' \neq k} \left\{ a(i,k') + s(i,k') \right\}\)
- E’ quindi aggiornata la disponibilità per
\(a(i,k) \leftarrow \min \left\{ 0, r(k,k) + \sum_{i' \not\in \{i,k\}} \max \left\{0, r(i',k)\right\} \right\}\) per \(i \neq k\) e
\(a(k,k) \leftarrow \sum_{i' \neq k} \max\left\{0, r(i',k)\right\}\).
Le iterazioni proseguono finché i confini dei cluster rimangono invariati per un certo numero di iterazioni, oppure dopo un numero predeterminato di iterazioni. Gli exemplar sono estratti dalle matrici finali come quei punti la cui “responsibilità + disponibilità” per loro stessi è positiva (cioè \((r(i,i)+a(i,i))>0\)).